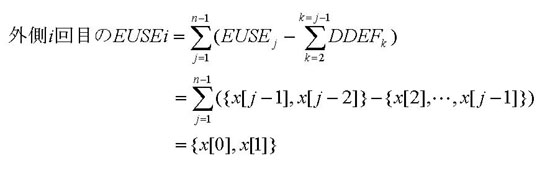7.1.1 ループ並列化の概要
並列化の基本機能として、ループの並列実行が可能であるかを判定する機能を持っている。
判定結果は中間表現HIRに反映させる。その結果を
- OpenMP指示文を追加したCソースプログラムとして出力することが出来る。
それを、既存のOpenMPコンパイラを通すことにより、並列に実行させることができる。
- LIRに変換し、並列マシン向けのの目的コードを生成することが出来る。
並列化は、コンパイラだけでは完結しない。コンパイラでは、並列実行するための
指示文の挿入や、並列実行のための制御ルーチンの呼び出し文を追加するにとどまる。
実際に並列実行させるには、言うまでもないことであるが
- 並列実行の機能を持つコンピュータ
- 並列実行の制御を行うOS、あるいは並列実行制御ルーチン
などを必要とする。OpenMP指示文を追加する場合には、COINS
で出力したCプログラムをさらに OpenMPコンパイラで処理しなければならない。
並列マシン向けの目的コードを出す場合には、並列実行制御ルーチンの
呼び出し文が追加されたコードが生成されるので、使うマシンに
合わせた並列実行制御ルーチン群を用意しなければならない。
並列化の対象としたのは次のループである。
- ループ内に入出力を含なまい。
- ループ外飛び出しやループ飛び込みがない。
- ユーザ定義関数(手続き)呼び出しがない。
- 構造体とポインタは解析対象外とする。ただし、FORTRANの実装では
COMMONや複素数を構造体として表現しているので、その
表現の構造体要素は解析対象とする。
プログラム全体の中で、並列化できる部分は限られている。
また、並列化して効果があるか否かを判定することは、
ループ反復数などの情報がなければできない。したがって、
入力されたプログラムを完全に自動並列化することは困難なので、
7.1.3.1小節で説明するように、並列化対象を含む副プログラムと、
その中で並列化の候補とするループを指示文(プラグマ)で
指定する必要がある。
実装されているのは、ループ繰り返しの(do-all型)並列実行の判定だけであるが、
そのために開発したデータフロー解析情報を使えば、以下のような応用を実装するのも比較的容易であると思われる。
たとえば、最内側ループの解析ではベクトル型の文並列化可否(ループ分割)の判定処理が可能である。
解析したフローグラフのパスに付随する参照領域から、変数と配列についてのデータ依存グラフの構築が可能であり、これを用いるとさらに広範囲なプログラム変換の可能性を探ることができる。さらに解析情報をサブプログラムの外へ渡すことを可能とすれば、モジュール間の並列化解析の研究にも活用可能である。
7.1.2 ループの解析と並列化変換
7.1.2.1 解析と並列化変換の方針
並列化可否判定のためのデータフロー解析は、最内側ループから、外側に向かって行う。
制御フローグラフのパスに沿ってデータのアクセス領域をまとめながら、最終的には一つのコンパイル単位である関数
(または手続き)全体でのアクセス領域を解析する。
ループのi回目の実行とj回目の実行で(ただしi≠j)の定義と使用、または定義と定義で同じ領域をアクセスする
可能性を検出した場合は、原則として並列化不可能と判定する。
ただし、それだけで判定すると、並列化不可能と判定されるものが多くなりすぎる。
そこで、並列化可能と判定するループを増やすために、以下のような基本的な並列化変換を行う.
- 基本インダクション変数変換
i = i + 定数
の代入文で表現される基本インダクション変数はループ繰返しに線形であると判断した場合は、
「初期値、増分値、ループ繰返し回数」を用いる式に変形し、独立な演算に変形する。
- リダクション命令の適用
s=s+<sを含まない式>
の代入文で表現される総和計算は、リダクション命令を適用できる。
このようなリダクション命令を適用できると判断した場合は、OpenMP 指示文にそのリダクション命令を指定して並列化する。
- private化
ループ内で使用するデータは、ループ本体で先立って定義され、ループ繰返しをまたぐ値を定義・使用することが無いと判定
した場合は、一つの変数(または配列)を繰返し回数ごとに一時的に用意するprivate化を行う。
並列化可否の判定も、解析に合わせて最内側から順に外側のループの判定を行う。並列化不可能と判定した場合は、
その要因となるデータの名称を出力する。並列化可否の判定結果と必要な指示(リダクション命令やprivate化)は、
中間表現の木にOpenMP指示文であることを示す非実行文のノードで反映させる。HIRからCソースプログラムを生成
するツールにより、これらはループに付随したOpenMP指示文として出力される。
以下、データフロー解析に用いた参照領域を説明し、各処理方式の概要を示す。
7.1.2.2 データの参照領域の解析
データフローの解析は基本的に制御フローグラフに沿って、基本ブロックから、ループi回目、ループ全回、関数全体で、
どの領域をどのような順序でアクセスするのかを解析していく。
7.1.2.2.1 参照領域情報
データの参照領域として、次の4種類に分類する。
- 可能性使用(USE)
ある範囲(フローグラフのパス)で、使用される可能性のあるデータ
- 可能性露出使用(EUSE:Exposed USE)
ある範囲(フローグラフのパス)で、定義に先立って使用される可能性のあるデータ
- 可能性定義(MOD:MODified)
ある範囲(フローグラフのパス)で、更新される可能性のあるデータ
- 確定定義(DDEF:Definitely Defined)
ある範囲(フローグラフのパス)で、必ず更新されるデータ
可能性使用と可能性定義はフローインセンシティブな情報であり、可能性露出使用と確定定義はフローセンシティブな情報である。
データアクセスの分類は様々な方法が提案されているが、ここでは、do-allループの検出を行うために、最内側ループだけではなく、
外側ループについてもループ繰越し依存関係の有無を判定できるように、また、将来の手続き間解析に備えて、
関数全体の参照領域を検出できるよう、上記のように決めた。
これらの領域は、次のような関係になる。
可能性使用 ⊆ 可能性露出使用
可能性定義 ⊆ 確定定義
可能性使用や可能性定義を求めているのは、後述の解析手法からも分かるとおり、安全側に倒すように判定を行うために
必要になるからであり、領域の結びや交わり、減算を計算を行うためには、ある程度のまとまりとして領域を保持したいためである。
7.1.2.2.2 配列の添え字の正規化
配列の添え字は次のように分類する。最内部に現れる配列は“範囲なし”の添え字となる。“範囲付き”となるのは、
内部にループ含む外側ループを解析するときに、内側ループ可変な添え字でアクセスされる場合である。
ここで、単にループというのは、並列化判定対象ループで、内側ループというのは、そのループが内包するループを指す。
添え字式は次のように分類される。
- ループ不変
- 範囲なし(ある一つの要素、内側ループ不変) [定数または、ループ不変式]
- 範囲付き(内側ループ可変)
- 内側ループのインダクション式 [ループ不変初期値,ループ不変終値,ループ不変増分値]
- 上記以外の内側ループ可変 USE、EUSE、MODは全要素、DDEFは空
- ループ可変
- 範囲なし(ある一つの要素、内側ループ不変)
- インダクション式 [ループ不変初期値,ループ不変終値,ループ不変増分値]
- 上記以外(ループ繰返しに非線形で可変、間接インデックスなど) USE、EUSE、MODは全要素、DDEFは空
- 範囲付き(内側ループ可変)
- 多次元配列で、ある一つの次元がインダクション式で、それ以外の次元は範囲付ループ不変
- 上記以外 解析不可能 USE、EUSE、MODは全要素、DDEFは空
- ループ範囲可変(例外的) 初期値か終値がインダクション式であるインダクション範囲
[ループ不変初期値,ループ可変終値,ループ不変増分値] または[ループ可変初期値,ループ不変終値,ループ不変増分値]
さらに[ループ可変初期値]や[ループ可変終値]は、[ループ不変初期値,ループ不変終値,ループ不変増分値]の組で表現する.
c. の例外的なループ範囲可変は、行列計算の時の上三角や下三角の領域を定義するために分類した。
2次元配列に対して、外側ループを解析するときだけこのパタンを見つけて、特別な処理を行う。
インダクション式を初期値か終値のどちらか一方しか許していないので、行列帯行列や対角要素に関する
アクセス領域の解析は行っていない。今後これらも三角要素と合わせて解析対象にする必要があるかもしれない。
これらの分類をより細密にして、各領域集合の加減算や積演算を定義すると、解析精度が高くすることができる。
これらの添え字の正規化のために、インダクション変数を検出し、標準化する。
7.1.2.3 基本インダクション変数の検出と変換
多くのループに現れる基本インダクション変数定義は、そのまま実行すると常にループの直前の値を参照して
新しい値を計算することになる。このままでは、ループの繰返しを並列に実行することができない。
そこで、OpenMPの並列実行時ルーチンが制御に用いているループ繰返し回数を利用して、
再帰性を除去した定義に変換して並列化適用範囲を広げることにした。
7.1.2.3.1 変換可能な基本インダクション変数
次の条件を満足した基本インダクション変数定義文は、再帰性を除去することができる。
- 定義文はループ繰返し部の中にはただ一つ
- 定義文はループ出口(解析対象ループは唯一つの出口を持つ)を支配
このような条件を設けたのは、基準となるインダクション変数で表現するためである。
1.の条件は、変換処理を用意することにより緩和させることができるが、2.は本質的である。
FortranのDOループの制御変数や、図7.1-1のように記述したforループの制御変数は、
必ずこれらの条件を満足する。
ここで検出したインダクション変数に対して、初期値設定用に作った処理系定義の変数と、
その定義式より見つけた増分値をテーブルに登録しておく。これらのインダクションテーブルは、
ループ単位の処理なのでループテーブルに接続する。
7.1.2.3.2 インダクション変数変換
基準となるインダクション変数e 「初期値:0、終値:ループの全繰返し回数−1、増分値:1」を
ループ制御変数として導入し、これをforループのループ制御変数とする。
次に前節の条件を満たすユーザ記述の基本インダクション変数定義をこのeを用いた式で置き換える。
既存のユーザ記述の基本インダクション変数のループ実行前の値を処理系が作成する一時的な変数
に代入する初期値設定文を、ループの直前に挿入する。
次に、基本インダクション変数の定義文をeを用いて再帰性のない次の定義文
基本インダクション変数=e*増分値+初期値の一時的な変数
に置き換える。
たとえば、図7.1-1ではfor文のループ制御変数iと繰返し部で定義しているjが適用対象である。
これらの代入文をeを用いて表現する。ループの直前にiとjのループ実行前の値を処理系作成の
一時的な変数に代入する初期値設定の文を挿入する。
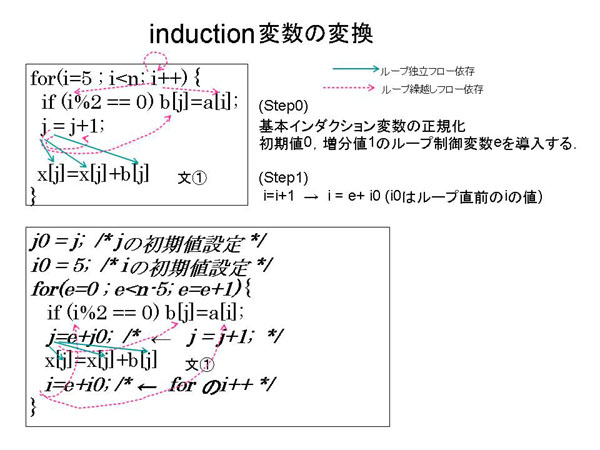
図7.1-1 基準インダクション変数の導入
その後、置き換えた基本インダクション定義文を繰返し部の先頭に移動する。
定義文から再帰性を除去しても、他の使用に対してループ繰越しフロー依存があると並列化できないため、
全てのフロー依存がループ独立となるよう繰返し部の先頭に移動する。
このとき、もともとループ独立なフロー依存がある場合は、その基本インダクション変数の使用を
「基本インダクション変数+増分値」で置き換える。これは、導入した基準インダクション変数eの
初期値が0であるためである。図7.1-1の例だと、図7.1-2のようになって、iやjにかかわる全ての
フロー依存はループ独立となり、インダクション変数変換が終わる。
この過程で、全ての基本インダクション変数とそれらを用いたインダクション式は初期値と増分値
で表現することが可能となり、配列の添え字式に対してはインダクション式であることと、その
[初期値,増分値,終値]の組をテーブルに保存する。

図7.1-2 定義文の移動と使用の置き換え
7.1.2.3.3 リダクション命令適用の検出
基本インダクション変数と条件が似ていて、ソース表現のままだと並列化することができないが、
特殊なリダクション命令を適用することにより並列化することができる計算がある。
総和に代表される交換則を適用できる計算である。
次の条件を満足する場合は、適用対象となる。
- その変数に対する代入は、対象ループ内で唯一でループ出口を支配している。
- 左辺変数の型はfloat、double、int、long、unsigned など数値を保持ずるもの。
- 代入左辺からの定義使用連鎖は唯一、同じ代入文の右辺式のただ一箇所に届く。
(s= s+s+a[i]は対象外ということ。)
これが基本インダクション変数より、厳しい条件である。
- 加算と乗算、減算を対象とする。
検出したリダクション命令適用演算は、リダクションテーブルとしてループテーブルに演算の種類とデータを登録して保持する。
当該ループの参照領域を解析した後、並列化不可能な要因がすべてリダクション命令の適用で解消可能である場合
はループ並列化可能と判断する。このときは、並列化指示のOpenMPの指示文にリダクション命令使用のオプションを付加する。
7.1.2.4 参照領域情報の解析
制御フローに沿って、文の単位から、基本ブロック、ループ、関数全体へ、並列化の判定に必要なデータ参照領域を計算する。
7.1.2.4.1 文における参照領域
一つの代入文では、代入左辺に現れるデータ(単純変数、配列要素)がMODとDDEFの構成要素になる。
代入右辺やループの繰り返し条件、if文の条件式に現れるデータ(単純変数、配列要素、配列の添え字式に現れる変数)
がUSEとEUSEの構成要素になる。
代入左辺が配列要素の場合は、その添え字式に現れる変数や配列要素はUSEとEUSEになる。
図7.1-3の文s1や文s2を参照されたい。
7.1.2.4.2 基本ブロックにおける参照領域
基本ブロックは、文が連続して並ぶので、各文の参照領域を次のようにまとめる。
文s1が文s2の実行に先立つとき、
USE(s1:s2) ← USE(s1)+USE(s2)
EUSE(s1:s2) ← EUSE(s1)+( EUSE(s2)−DDEF(s1) )
MOD(s1:s2) ← MOD(s1)+MOD(s2)
DDEF(s1:s2) ← DDEF(s1)+DDEF(s2)
と、計算する。"+"は和集合、"−"は差集合(共通部分を除く)、"*"は積集合を表す。
ここで、EUSEの( )は重要である。必ず加算より先に、( EUSE(s2)−DDEF(s1) )の計算をする必要がある。
たとえば次の3つの文がひとつの基本部ブロックを構成するとき、前節に記した方法で、次のように各参照領域が決まる。
a = a + c … /s1/ USE(s1)=EUSE(s1)={a,c},MOD(s1)=DDEF(s1)={a}
b = c + d … /s2/ USE(s2)=EUSE(s2)={c,d},MOD(s2)=DDEF(s1)={b}
a = b + c … /s3/ USE(s3)=EUSE(s3)={b,c},MOD(s3)=DDEF(s1)={a}
これらについて、まず文s1と文s2のEUSEを求める。
EUSE(s1:s2) ← EUSE(s1)+( EUSE(s2)−DDEF(s1) )={a,c}+( {c,d}−{a} ) = {a,c,d}
このときに、( {c,d}−{a} )では、共通部分が無いため、実質減算は行われず、変数aはEUSEに残る。
( )が無いとaまで消えてしまう。
文s1のaの使用は、全てのaの定義に先立つ露出使用である。
DDEF(s1:s2) ← DDEF(s1)+DDEF(s2) = {a,b} となるため、
EUSE(s1:s2:s3) ← EUSE(s1:s2)+( EUSE(s3)−DDEF(s1:s2) )= {a,c,d}+({b,c}−{a,b}) = {a,c,d}
({b,c}−{a,b})から、変数bは削除され、cだけが残る。その結果、この基本ブロックで定義に先立つ使用は
a、c、dであることがわかる。
配列要素が用いられている、文の参照領域と基本ブロックの参照領域の例を図7.1-3に示す。
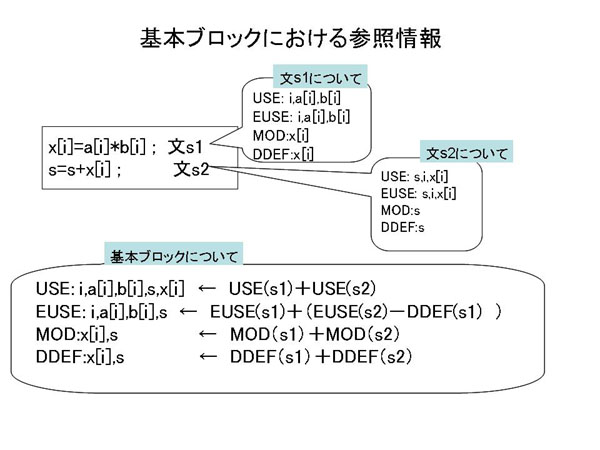
図7.1-3 基本ブロックの参照領域
7.1.2.4.3 最内側ループi回目の参照領域
いずれのループの並列化可否を判定したい場合でも、データフローの解析は必ず最内側から行う。
ループ繰返し部(ループボディ)のフローグラフに沿って、基本ブロックごとの参照領域を一つにまとめ、
ループi回目の参照領域を求める。これは、再帰呼出しを用いてフローグラフを深さ優先でたどり、
条件分岐による枝分かれがあると図7.1-4の統合(条件分岐)を行い、この処理により連接する参照領域ができると
、図7.1-5の統合(連接)処理を行って一つにまとめる。連接する参照領域の統合は基本ブロック内の連続する文
の参照領域の統合と同じである。
"+"は和集合、"−"は差集合(共通部分を除く)、"*"は積集合を表す。
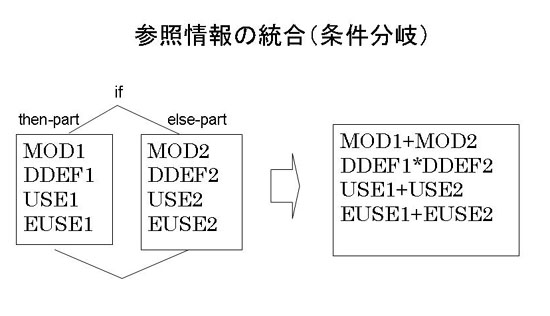
図7.1-4 条件分岐の参照領域の統合
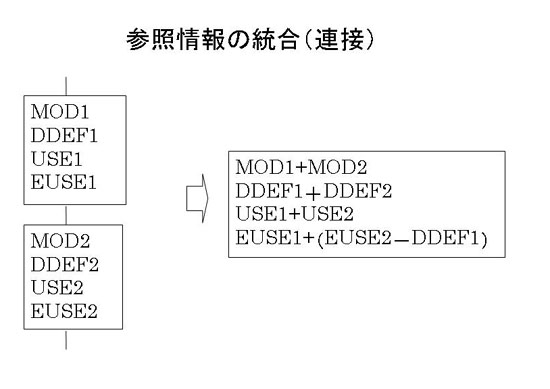
図7.1-5 連接する参照領域の統合
制御フローグラフの基本ブロックごとの参照領域を、これらの2種類の統合処理を施して、
並列化を判定する当該ループのあるi回目の参照領域を計算する。
7.1.2.4.4 並列化判定対象ループ全回の参照領域
単純変数は、ループのあるi回目の実行でも、ループ全回の実行でもアクセス領域が等しいが、
ループ可変である添え字でアクセスする配列は、各回ごとにアクセスする要素が異なる。
そのため、ループを全て実行したときの参照領域も用いる。これは、次の節に記す判定対象ループ
が内包する内側ループの展開とは異なる。
単純に正規化したループ繰返し回数について、初期値から終値までシグマをとる。ただし、
解析できないループ可変な添え字式(ループ繰返しに非線形、間接指標アクセス)については、
全領域か空領域かの安全側に倒す。

7.1.2.4.5 内側にループを含むループの解析
当該ループに関するインダクション変数を検出し、初期値、終値、増分値を解析し、
インダクション変数変換を行うのは最内側の時と同様である。これにより、配列添え字式の標準化を行う。
最内部の解析は、最内側ループと同様である。
内側ループに現れた配列の要素アクセスは、解析ループが異なるとその各繰返しでのアクセス範囲も当然異なる。
ループ繰返し部に定義文があり、ループ可変と判定する変数にも、内側ループのインダクション変数
のように特定の範囲を規則的に変化するものと、純粋に新たに値が定義されるループ可変変数がある
ことが分かる。そこで、内側ループの解析結果を用い表7.1-1ののようにして、外側ループのために
配列の添え字式を新たに2.2節のように分類する。
内側不変式の例を図7.1-6に、内側インダクション式の例を図7.1-7に示す。
表7.1-1 内側ループと外側ループでの添え字式分類
| 内側ループ |
外側ループ |
例 |
| 不変式 |
不変式 |
図7.1-6のc[m] |
| インダクション式 |
図7.1-6のa[j] |
| 解析不可能式 |
図7.1-6のb[k] |
| インダクション式 |
範囲付不変式 |
図7.1-7のa[i] |
| インダクション範囲 |
図7.1-7のc[m] |
| 解析不可能範囲 |
図7.1-7のb[k] |
| 解析不可能式 |
解析不可能範囲 |
|
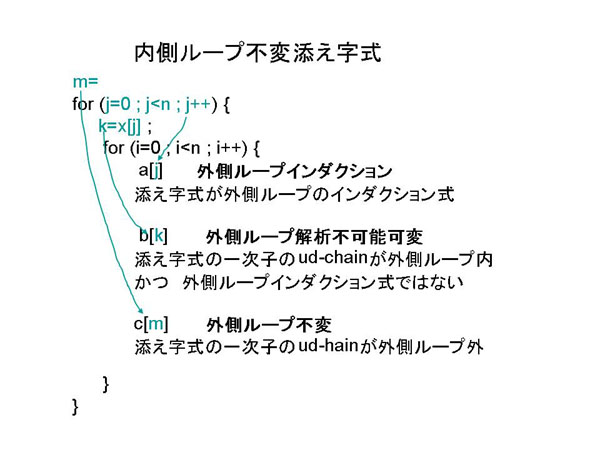
図7.1-6 内側ループ不変添え字の分類

図7.1-7 内側インダクション添え字式の分類
内側にループを含むループの並列化可否を判定する場合は、内側ループの参照領域をまとめる必要がある。
内側ループのある1回の参照領域と、それから導かれる全回の参照領域はすでに計算されている。
原理的には連接する基本ブロックの統合と同じである。図7.1-8に示す。
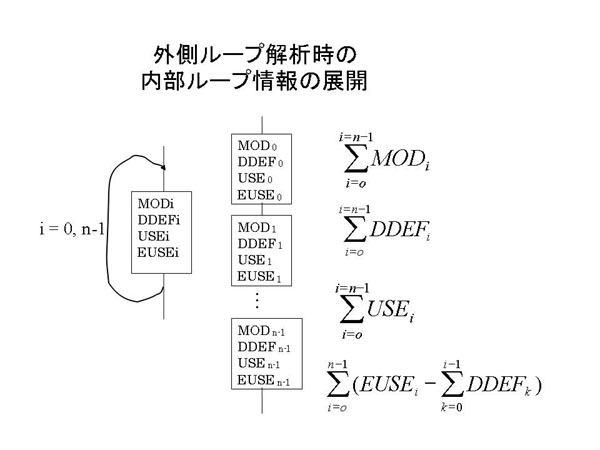
図7.1-8 外側ループ解析時の内側ループの参照領域の展開
内側ループi回目のEUSEを求めるのに、0回目から(i-1)回目までのDDEFの和集合を除き、
それを内側ループの全回で加えたものが、一つ外側から見た内側ループブロックにおける露出使用となる。
このようにして、展開した内側ループの参照領域を、並列化可否判定対象としている外側ループの最内部の
参照領域とまとめる。これは、4.4節の基本ブロック間の統合と等しい。
内側ループを一つの基本ブロックのように扱うわけである。
その様子を図7.1-9に示す。
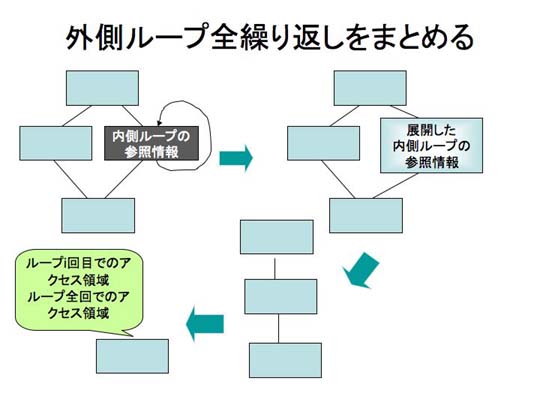
図7.1-9 内側にループを持つループの参照領域のまとめ
この解析により、内側ループでは繰越し依存関係にあったものが、外側ループから見ると、
private化することにより並列化可能と判断できる場合がある。7.1.2.6節に例を示す。
7.1.2.4.6 関数(手続き)全体の参照領域
前述のようにして、最内側ループから外側に向けてデータの参照領域をまとめ、各ループについて並列化可否を判定する。
最終的には一つの関数(手続き)全体での参照領域を解析し、他の関数(手続き呼出し)の有無とその関数名、
グローバルデータに関する参照領域、仮引数に関する参照領域、の3種類の情報を関数ごとにファイル出力する。
情報は、安全側に倒されたもので、MOD、USE、EUSEは可能性のある最大領域を、DDEFは確実に定義される
最小領域を示している。
- 他の関数(手続き呼出し)
このファイルの参照領域が閉じたものか、そうでないのかを表すために必要である。呼び出しているユーザ定義関数の
種類と名称を並べる。
- 仮引数に関する情報
関数全体を解析した結果のUSEとEUSEの参照領域にある仮引数の領域と、MODとDDEFの各参照領域では
アドレス渡しの仮引数(Cだと配列名称、Fortranだと仮引数全て)の領域を並べる。
- グローバルデータに関する参照領域
関数全体を解析した結果のUSE、EUSE、MOD、DDEFの各参照領域で、グローバルデータの領域を並べる。
7.1.2.4.7 領域の演算
本システムでは、6.6.2節にも記したように配列の添え字を分類したので、これら「ループ不変」「インダクション式」
「ループ可変解析不可能」の添え字の組み合わせについて、領域の和、積、差をとる処理と、大小比較、
同値判定の処理を用意している。これらは5.章に示す判定処理において必要になる。
現在はソース表現(中間表現)のパタンマッチで行っているが、数式処理などの手法を取り入れると
、解析精度を向上させることができる。
7.1.2.5 並列化可否の判定
各繰返しを独立に並列実行できるdo-allループを検出する。このために、異なる繰返し回で同じデータ領域に
定義・使用、定義・定義が発生するループ繰越し依存(フロー、逆、出力)の有無を判定する。
ただし、前述のようにリダクション命令やprivate化によって繰越し依存が解消されるものも検出し、
これらは並列化不可能要因からはずす。
7.1.2.5.1 変数に関する判定
変数は値を使用したり定義する場合、そのアドレス(領域)は等しい。従って、
常に異なる繰返し回で同じアドレス(領域)をアクセスすることになり、ループ繰越し依存が生じる。
ループi回目の参照領域から、次の原則に従って、ループ繰越し依存有無の判定を行う。
(a) EUSEi ∩ MODi ≠{Φ} ループ繰越しフロー依存がある。
(b) USEi ∩ MODi ≠{Φ} ループ繰越し逆依存がある。
(c) MODi ≠{Φ} ループ繰越し出力依存がある。
図7.1-10に変数のループ繰越し依存の例を示す。
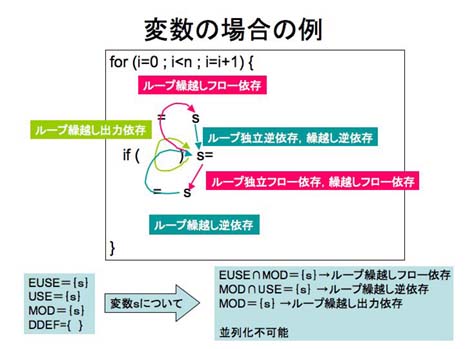
図7.1-10 変数のループ繰越し依存関係
ループ繰越し依存関係のうち、private化することによって、ループ繰越し出力依存とループ繰越し逆依存は解消できる。
ただし、private化することができるのは、ループ繰越しフロー依存が無い場合だけである。図7.1-10の例では、
ループ繰越しフロー依存があるためprivate化することはできない。図7.1-11にprivate化により並列化可能となる例を示す。
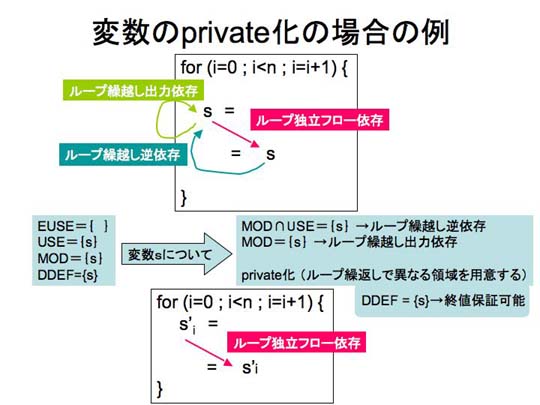
図7.1-11 変数のprivate化によってループ繰越し逆依存と出力依存を解消する例
ループ繰越し依存を検出しても、リダクション命令を用いることにより並列に実行できることがテーブルに登録されている場合は、
並列化不可能要因からはずし、OpenMPの指示文にリダクション命令に関するオプションを加える。
ループ不変な添え字式でアクセスされる配列要素は、ここに示した単純変数と同様に扱うが、配列の要素単位でprivate化
する手段が無く、配列全体をprivate化する場合のオーバヘッドが大きくなることから、private化による並列化は行わず、
並列化不可能と判断している。
7.1.2.5.2 配列に関する領域参照領域とループ繰越し依存
領域に関するデータ参照領域と、配列についてのループ繰越し依存の有無は、次のように定義することができる。
 次に、ここまで記してきた解析方法と判定方法を用いて、並列化可否を判定し、OpenMPソースプログラムを
生成する例をあげる。
次に、ここまで記してきた解析方法と判定方法を用いて、並列化可否を判定し、OpenMPソースプログラムを
生成する例をあげる。
7.1.2.6 解析とソースプログラム生成の実行例
実際の二重ループの解析例と変換結果である出力のC+OpenMPのソースプログラムを示す。
内側のループを解析した結果並列化不可能と判断するが、その外側まで解析すると、
外側ループについては並列に実行できると判断できる例である。
図7.1-13に内側ループについて解析した参照領域と、それによって並列化不可能と判定する様子を示す。
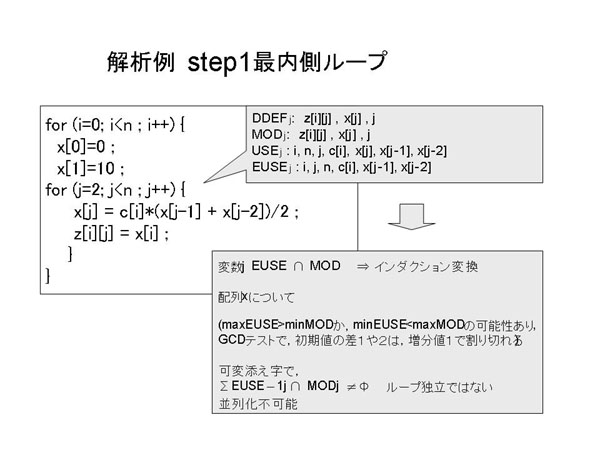
図7.1-12 内側ループの参照領域と並列化可否判定結果
次に外側ループの解析のために内側ループの情報を展開する。EUSE以外はそのまま全回繰返しの領域
になるよう和集合をとる。
EUSEについては、
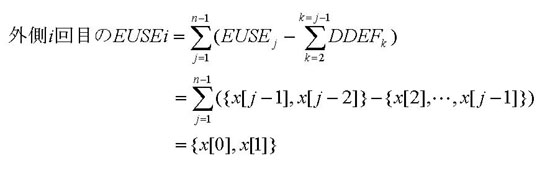 となる。j=2とj=3のときに使用するx[0]とx[1]の要素だけがこの内側ループの全回実行で露出使用されていることがわかる。
この結果外側ループの情報と統合するための内側ループの全回繰返しでの参照領域は図7.1-13のようになる。
となる。j=2とj=3のときに使用するx[0]とx[1]の要素だけがこの内側ループの全回実行で露出使用されていることがわかる。
この結果外側ループの情報と統合するための内側ループの全回繰返しでの参照領域は図7.1-13のようになる。
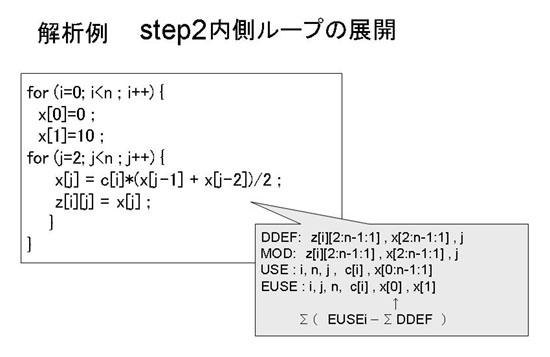
図7.1-13 内側ループの参照領域の展開
最後に外側ループの最内部と内側ループ部の参照領域を図7.1-14のように統合して、外側ループの並列化可否を判定する。
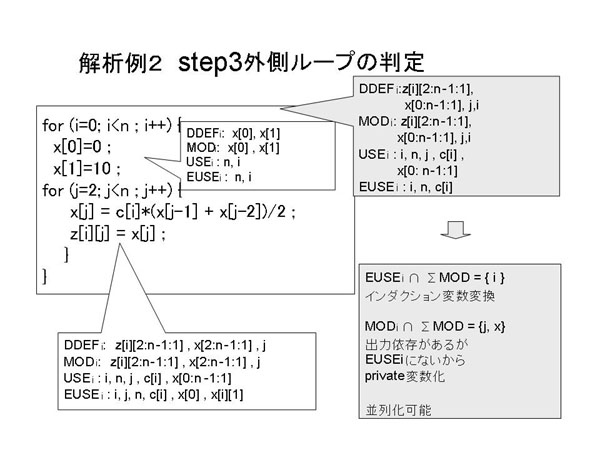
図7.1-14 参照領域の統合と外側ループ並列化可否の判定
外側ループの最内部の配列xの要素x[0]とx[1]への定義文があり、これらがMODとDDEFになる。連接する参照領域の統合で、
EUSE外側ループi回目=EUSE内側ループ−DDEF最内部
を求めると、
EUSE外側ループi回目= {Φ}
となる。一方、MODは
MOD外側ループi回目=MOD最内部+MOD内側ループ
なので、
MOD外側ループi回目= { x[0:n-1:1] } (範囲付きループ不変)
となる。
EUSE外側ループi回目 ≠ MOD外側ループi回目
であることから、ループ独立ではない、繰越し依存があると判断して並列化不可能で、その要因に配列xを提示する。
また、USE領域については、
USE外側ループi回目={ x[0:n-1:1] } (範囲付きループ不変)
である。
 外側ループについてEUSEとMODに重なりがないこと、また、MODとUSEの領域は、範囲はあるが外側ループ不変で、
かつその範囲が等しいことから、ループ繰越しフロー依存関係が無いことがわかる。
MODとUSEの領域が外側ループ不変領域であるため、単純変数と同様に毎回同じ領域をアクセスするため、
ループ繰越し逆依存とループ繰越し出力依存が存在するが、これは配列xをprivate化することによって解消することができる。
外側ループについてEUSEとMODに重なりがないこと、また、MODとUSEの領域は、範囲はあるが外側ループ不変で、
かつその範囲が等しいことから、ループ繰越しフロー依存関係が無いことがわかる。
MODとUSEの領域が外側ループ不変領域であるため、単純変数と同様に毎回同じ領域をアクセスするため、
ループ繰越し逆依存とループ繰越し出力依存が存在するが、これは配列xをprivate化することによって解消することができる。
図7.1-15に並列実行のためのOpenMP指示文を挿入した出力ソースプログラムを示す。
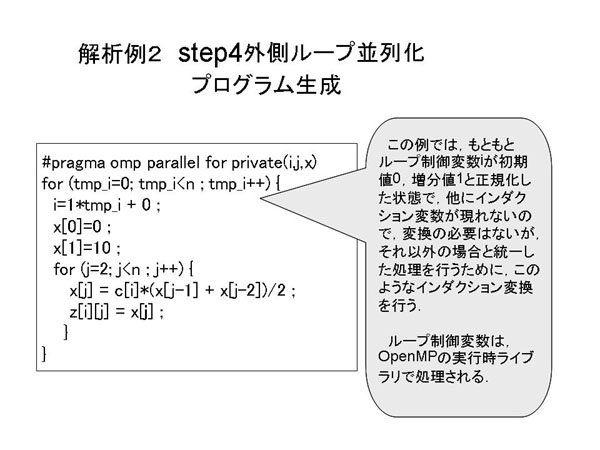
図7.1-15 生成するC+OpenMP指示文のソースプログラム
7.1.2.7 解析・変換の実現方法とツールとしてのモジュール化
ここで実現した並列化のための解析処理や変換処理は、COINSの提供する基盤部を用いる環境では、
モジュールとして独立して使用したり、また、性能を向上させるために別途開発されたものを置き換えることができる。
ツールとしてモジュール化できる機能には次のようなものがある。
- サブプログラム単位のループ解析
- サブプログラム単位のループ変換
- サブプログラム単位の OpenMP 化
- サブプログラム単位のデータアクセス領域解析
これらのモジュールを組合わせて用いることにより、個別のアプリケーションや個々のターゲット並列計算機に
向けた並列化コンパイラを効率よく開発することができる。
7.1.3 OpenMPコンパイラとの連携
7.1.3.1 並列化候補の指定
既に述べたように、並列化の結果をOpenMP指示文を追加したCプログラム
(OpenMP拡張Cプログラム)として出力し、
それを既存のOpenMPコンパイラに渡すことにより、並列実行させることができる。
一般に、並列化によって高速化できるか否かを自動判定するのは容易でないので、
COINSのループ並列化では、ソースプログラム全体の並列化を試みるのではなく、
並列化の候補となるループをプラグマによって人手で指定してもらう。
ループ並列化部では、指定された候補ループを解析して本当に並列化できるか否か、
できる場合はどんな並列化が可能かを見定め、それに合わせた変換を行う。
並列化候補の指定では、コンパイル単位の先頭部分で、まず並列化候補を含む
ルーチン(関数)を次の形で指定する。
#pragma parallel doAllFunc func1 func2 ...
ここで、func1, func2, ... は並列化候補を含む関数の名前である。
コンパイル単位の全ての関数を対象とする場合は
#pragma parallel doAllFuncAll
と指定する。指定されていない関数に対しては、並列化の解析を行わない。
並列化の候補とするループの前には
#pragma parallel doAll
をおく。このプラグマの後ろで最初に出会ったforループが並列化の対象として
解析され、並列化できることがわかると、出力されるCプログラムの中に、
並列化のやりかたを示すOpenMP用のプラグマが挿入される。
1つのプラグマは複数行に分けないで1行に書く。
7.1.3.2 並列化されたCプログラムの生成
OpenMP向けに並列化されたCプログラムの生成まででCOINSの処理を終える場合は、
次のようなコンパイルコマンドを与える。
java coins.driver.Driver -coins:parallelDoAll=OpenMP foo.c
そうすると、入力プログラムが foo.c であれば、その名前の後ろに-loopをつけた
foo-loop.cというCプログラムが生成されるので、それをOpenMPの処理系に
入力すれば並列実行ができる。
例として、次のプログラム
#pragma parallel doAllFunc main
int printf(char*, ...);
int k, c[50];
main()
{
int x[50];
int i, j, n, sum;
n = 50;
k = 100;
sum = 0;
#pragma parallel doAll
for (i = 0; i < n; i++) {
x[i] = k + i;
c[i] = i * i;
k = k - 2;
sum = sum + x[i];
}
for (j = 0; j < n; j++)
printf("x[%d]=%d c[%d]=%d", j, x[j], j, c[j]);
printf("\nk = %d sum = %d \n", k, sum);
return 0;
}
を入力すると、生成されるCプログラムは次のようになる。
extern int printf ( char * , ... ) ;
int k, c[50];
int main( )
{
int x[50];
int i, j, n, sum;
n = 50;
k = 100;
sum = 0;
#pragma omp parallel for lastprivate(k,i) reduction(+:sum)
for ( i = 0;i < n; i = i + 1)
{
k = (-2) * i + 100;
{
x[i] = k + i;
c[i] = i * i;
sum = sum + x[i];
}
}
_lab4:;
k = (-2) * i + 100;
for ( j = 0;j < n; j = j + 1)
{
(&(printf))( ("x[%d]=%d c[%d]=%d"),j,x[j],j,c[j]);
}
_lab8:;
(&(printf))( ("\nk = %d sum = %d \n"),k,sum);
return 0;
}
ここで、生成されたCプログラムは、そのままではマクロ(#define)が使われていたり
型修飾がすべての式についていたりしているので、見やすいように
整形してある。
7.1.3.3 並列化された実行モジュールの生成
COINSで生成したOpenMP拡張Cプログラムを引き続いてOpenMPコンパイラに入力し、
並列実行させることもできる。その場合は、COINSのコンパイラドライバを継承した
LoopParaと呼ぶドライバを使う。具体的には、コマンドラインから次の呼び出しで
実行可能モジュールを生成することができる。
java coins.lparallel.LoopPara -coins:hir2c foo.c
これでは、 COINSのループ並列化を呼び出し、並列化が可能であった場合、
OpenMP拡張Cプログラムを生成し、それをOpenMPコンパイラでコンパイル、リンクして
実行可能モジュールを生成する。
これでは、既存のOpenMPコンパイラとして OMNI (ompcc) を利用している。
7.1.4 並列マシン用の目的コード生成
これについては、別ページ
(並列マシン用コード生成の概要)に説明してある。